RSA is an algorithm for public-key cryptography that is based on the presumed difficulty of factoring large integers, the factoring problem. RSA stands for Ron Rivest, Adi Shamir and Leonard Adleman, who first publicly described the algorithm in 1977. Clifford Cocks, an English mathematician, had developed an equivalent system in 1973, but it was classified until 1997.
A user of RSA creates and then publishes the product of two large prime numbers, along with an auxiliary value, as their public key. The prime factors must be kept secret. Anyone can use the public key to encrypt a message, but with currently published methods, if the public key is large enough, only someone with knowledge of the prime factors can feasibly decode the message.[1] Whether breaking RSA encryption is as hard as factoring is an open question known as the RSA problem.
| To do this | Use whose | Kind of key |
| Send an encrypted message | Use the receiver's | Public key |
| Send an encrypted signature | Use the sender's | Private key |
| Decrypt an encrypted message | Use the receiver's | Private key |
| Decrypt an encrypted signature (and authenticate the sender) | Use the sender's | Public key |
The RSA algorithm involves three steps: key generation, encryption and decryption.
Key generation
RSA involves a public key and a private key. The public key can be known to everyone and is used for encrypting messages. Messages encrypted with the public key can only be decrypted in a reasonable amount of time using the private key. The keys for the RSA algorithm are generated the following way:- Choose two distinct prime numbers p and q.
- For security purposes, the integers p and q should be chosen at random, and should be of similar bit-length. Prime integers can be efficiently found using a primality test.
- Compute n = pq.
- n is used as the modulus for both the public and private keys. Its length, usually expressed in bits, is the key length.
- Compute φ(n) = (p – 1)(q – 1), where φ is Euler's totient function.
- Choose an integer e such that 1 < e < φ(n) and gcd(e, φ(n)) = 1; i.e., e and φ(n) are coprime.
- e is released as the public key exponent.
- e having a short bit-length and small Hamming weight results in more efficient encryption – most commonly 216 + 1 = 65,537. However, much smaller values of e (such as 3) have been shown to be less secure in some settings.[4]
- Determine d as d ≡ e−1 (mod φ(n)), i.e., d is the multiplicative inverse of e (modulo φ(n)).
-
- This is more clearly stated as solve for d given de ≡ 1 (mod φ(n))
- This is often computed using the extended Euclidean algorithm.
- d is kept as the private key exponent.
- An alternative, used by PKCS#1, is to choose d matching de ≡ 1 (mod λ) with λ = lcm(p − 1, q − 1), where lcm is the least common multiple. Using λ instead of φ(n) allows more choices for d. λ can also be defined using the Carmichael function, λ(n).
- The ANSI X9.31 standard prescribes, IEEE 1363 describes, and PKCS#1 allows, that p and q match additional requirements: being strong primes, and being different enough that Fermat factorization fails.
Encryption
Alice transmits her public key (n, e) to Bob and keeps the private key secret. Bob then wishes to send message M to Alice.He first turns M into an integer m, such that 0 ≤ m < n by using an agreed-upon reversible protocol known as a padding scheme. He then computes the ciphertext c corresponding to
Decryption
Alice can recover m from c by using her private key exponent d via computingA working example
Here is an example of RSA encryption and decryption. The parameters used here are artificially small, but one can also use OpenSSL to generate and examine a real keypair.- Choose two distinct prime numbers, such as
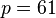 and
and 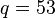 .
.
- Compute n = pq giving
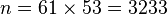 .
.
- Compute the totient of the product as φ(n) = (p − 1)(q − 1) giving
 .
.
- Choose any number 1 < e < 3120 that is coprime to 3120. Choosing a prime number for e leaves us only to check that e is not a divisor of 3120.
- Let
 .
.
- Let
- Compute d, the modular multiplicative inverse of e (mod φ(n)) yielding
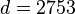 .
.
The private key is (n = 3233, d = 2753). For an encrypted ciphertext c, the decryption function is c2753 (mod 3233).
For instance, in order to encrypt m = 65, we calculate
 .
.

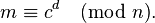

Excellent work ! Using this post I have understood the complete working of rsa algorithm. I am pleased that you used a working example to clear all the things so well. Appreciating !!
ReplyDeletedigital signature